Mastering Merge Sort: The Secret Weapon for Sorting Success!

Have you ever felt like you were drowning in a sea of numbers? Do you want to transform that chaos into clarity with just a sprinkle of coding magic? If you’re eager to learn how to sort arrays like a pro, then Merge Sort is your ticket to success! This blog will guide you through the fascinating world of Merge Sort, breaking it down into bite-sized pieces that are easy to digest.

What Is Merge Sort?

At its core, Merge Sort is a divide-and-conquer algorithm. It breaks down large problems into smaller, more manageable parts and then combines those solutions. Think of it as organizing a messy room: you start by sorting items into smaller piles before putting everything in its rightful place.

Why Merge Sort Matters

• Efficiency: Merge Sort boasts a time complexity of O(nlog⁡n)O(n \log n)O(nlogn), making it ideal for sorting large datasets quickly.
• Stability: It keeps the original order of equal elements, which is crucial for certain applications.
• Adaptability: It works wonders with both in-memory data and larger datasets that may not fit into memory.

Curious to Know How It Works?

Let’s embark on this sorting journey! Here’s how Merge Sort operates, step by step:

Step 1: Divide

The first step is to split the array into halves until you’re left with subarrays containing a single element. Why single elements? Because they are inherently sorted!

Step 2: Conquer

Once you have these tiny sorted pieces, it’s time to merge them back together. This is where the real magic happens!

Step 3: Combine

Keep merging the sorted subarrays until you rebuild the entire array in the correct order.

Given an array of size n, sort the array using Merge Sort.

Examples:

Example 1:
Input: N=5, arr[]={4,2,1,6,7}
Output: 1,2,4,6,7,


Example 2:
Input: N=7,arr[]={3,2,8,5,1,4,23}
Output: 1,2,3,4,5,8,23

Solution :

Intuition: 

1. Merge Sort is a divide and conquers algorithm, it divides the given array into equal parts and then merges the 2 sorted parts. 
2. There are 2 main functions :
   merge(): This function is used to merge the 2 halves of the array. It assumes that both parts of the array are sorted and merges both of them.
   mergeSort(): This function divides the array into 2 parts. low to mid and mid+1 to high where,

 low = leftmost index of the array
 high = rightmost index of the array
 mid = Middle index of the array

3. We recursively split the array, and go from top-down until all sub-arrays size becomes 1.

Approach : 

Approach:

• We will be creating 2 functions mergeSort() and merge().
• mergeSort(arr[], low, high):
  1. In order to implement merge sort we need to first divide the given array into two halves. Now, if we carefully observe, we need not divide the array and create a separate array, but we will divide the array’s range into halves every time. For example, the given range of the array is 0 to 4(0-based indexing). Now on the first go, we will divide the range into half like (0+4)/2 = 2. So, the range of the left half will be 0 to 2 and for the right half, the range will be 3 to 4. Similarly, if the given range is low to high, the range for the two halves will be low to mid and mid+1 to high, where mid = (low+high)/2. This process will continue until the range size becomes.
  2. So, in mergeSort(), we will divide the array around the middle index(rather than creating a separate array) by making the recursive call :
     1. mergeSort(arr,low,mid)   [Left half of the array]
     2. mergeSort(arr,mid+1,high)  [Right half of the array]
     where low = leftmost index of the array, high = rightmost index of the array, and mid = middle index of the array.
  3. Now, in order to complete the recursive function, we need to write the base case as well. We know from step 2.1, that our recursion ends when the array has only 1 element left. So, the leftmost index, low, and the rightmost index high become the same as they are pointing to a single element.
     Base Case: if(low >= high) return;

Pseudocode:

• merge(arr[], low, mid, high):
  1. In the merge function, we will use a temp array to store the elements of the two sorted arrays after merging. Here, the range of the left array is low to mid and the range for the right half is mid+1 to high.
  2. Now we will take two pointers left and right, where left starts from low and right starts from mid+1.
  3. Using a while loop( while(left <= mid && right <= high)), we will select two elements, one from each half, and will consider the smallest one among the two. Then, we will insert the smallest element in the temp array.
  4. After that, the left-out elements in both halves will be copied as it is into the temp array.
  5. Now, we will just transfer the elements of the temp array to the range low to high in the original array.

The pseudo code will look like the following:

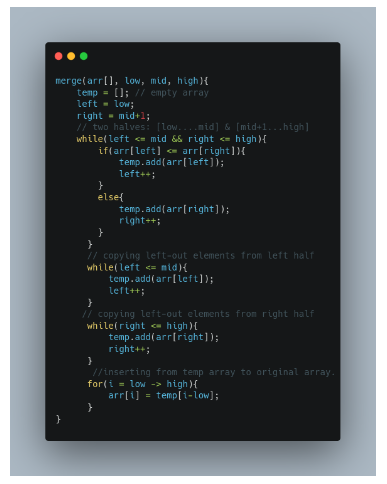
The red number shows the order of the steps in recursion calls.

Code:

Code:C++Java

#include <bits/stdc++.h>
using namespace std;

void merge(vector<int> &arr, int low, int mid, int high) {
    vector<int> temp; // temporary array
    int left = low;      // starting index of left half of arr
    int right = mid + 1;   // starting index of right half of arr

    //storing elements in the temporary array in a sorted manner//

    while (left <= mid && right <= high) {
        if (arr[left] <= arr[right]) {
            temp.push_back(arr[left]);
            left++;
        }
        else {
            temp.push_back(arr[right]);
            right++;
        }
    }

    // if elements on the left half are still left //

    while (left <= mid) {
        temp.push_back(arr[left]);
        left++;
    }

    //  if elements on the right half are still left //
    while (right <= high) {
        temp.push_back(arr[right]);
        right++;
    }

    // transfering all elements from temporary to arr //
    for (int i = low; i <= high; i++) {
        arr[i] = temp[i - low];
    }
}

void mergeSort(vector<int> &arr, int low, int high) {
    if (low >= high) return;
    int mid = (low + high) / 2 ;
    mergeSort(arr, low, mid);  // left half
    mergeSort(arr, mid + 1, high); // right half
    merge(arr, low, mid, high);  // merging sorted halves
}

int main() {

    vector<int> arr = {9, 4, 7, 6, 3, 1, 5}  ;
    int n = 7;

    cout << "Before Sorting Array: " << endl;
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " "  ;
    }
    cout << endl;
    mergeSort(arr, 0, n - 1);
    cout << "After Sorting Array: " << endl;
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " "  ;
    }
    cout << endl;
    return 0 ;
}

Output:

Before Sorting Array:
9 4 7 6 3 1 5
After Sorting Array:
1 3 4 5 6 7 9

Time complexity: O(nlogn) 

Reason: At each step, we divide the whole array, for that logn and we assume n steps are taken to get sorted array, so overall time complexity will be nlogn

Space complexity: O(n)  

Reason: We are using a temporary array to store elements in sorted order.

Auxiliary Space Complexity: O(n)

Code Breakdown

• Merge Function: This function merges two sorted halves into a temporary array.
• Merge Sort Function: This divides the array and recursively sorts the left and right halves.

Real-World Applications of Merge Sort

Merge Sort isn’t just an academic exercise; it has real-world applications:

• Database Management: Sorting large datasets efficiently.
• External Sorting: Ideal for sorting files that don’t fit into memory.
• Multithreading: Easily parallelized for modern computing environments.

Tips for Implementing Merge Sort

1. Start Small: Begin with small arrays to get comfortable with the process.
2. Visualize It: Draw diagrams to understand how arrays are split and merged.
3. Practice: The more you code, the better you’ll grasp the concepts.

Final Thoughts

Merge Sort might not be the flashiest sorting algorithm, but its efficiency and reliability make it a favorite among developers. By mastering this algorithm, you’ll equip yourself with the skills to handle sorting challenges with ease.

So, are you ready to sort your way to success?

Dive into the code, experiment, and watch the magic of Merge Sort unfold!

Happy coding!