Mastering the Recursive Bubble Sort Algorithm: A Step-by-Step Guide

Have you ever wondered how your favorite sorting algorithm works under the hood? Sorting algorithms are not just vital tools for programmers; they also play a crucial role in everyday applications, from organizing your playlists to optimizing search results. Today, we’re diving into the world of sorting with a focus on the Recursive Bubble Sort algorithm.

What is Bubble Sort?

At its core, Bubble Sort is a straightforward comparison-based algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. This process is repeated until the list is sorted. The beauty of Bubble Sort lies in its simplicity, making it an excellent choice for beginners learning about sorting algorithms. But how can we make this even more interesting? Let’s explore the recursive approach!

Why Choose Recursion?

Recursion allows us to solve problems by breaking them down into smaller subproblems. With Recursive Bubble Sort, we can leverage this concept to simplify our sorting process. Instead of using loops, we’ll make function calls that reduce the size of the unsorted portion of the array.

The Recursive Bubble Sort Approach

1. Base Case: If the size of the array (or the remaining unsorted portion) is 1, it’s already sorted, and we can return.
2. Bubble Up: For each call, iterate through the array and swap adjacent elements if they are out of order. After one complete pass, the largest unsorted element will “bubble up” to its correct position.
3. Recur: Call the sorting function again with a reduced size (n-1) until we hit our base case.

Dry Run: Let’s See It in Action!

Imagine we have the array: {13, 46, 24, 52, 20, 9}.

• First Call: Start with the entire array (n=6). The largest number (52) bubbles to the end.
• Second Call: Now consider the first five elements {13, 46, 24, 20, 9}. The next largest number (46) moves to its position.
• Continue: Repeat until only one element remains unsorted.

Here’s how the recursive calls would break down:

Recursion 1: bubble_sort(arr, 6):

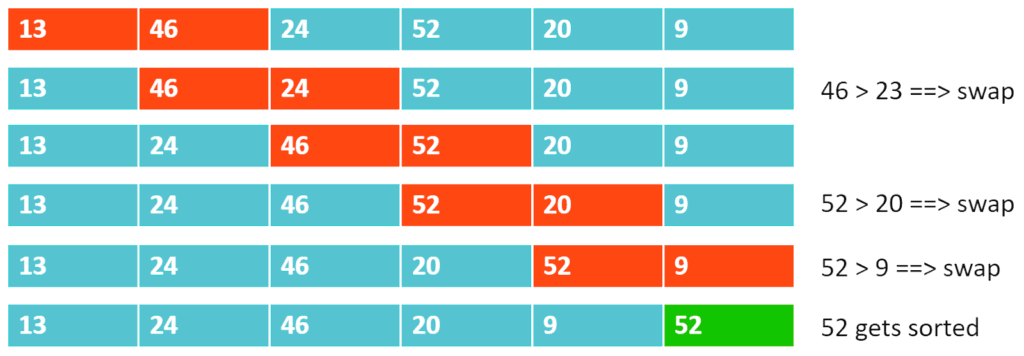
Recursion 2: bubble_sort(arr, 5):

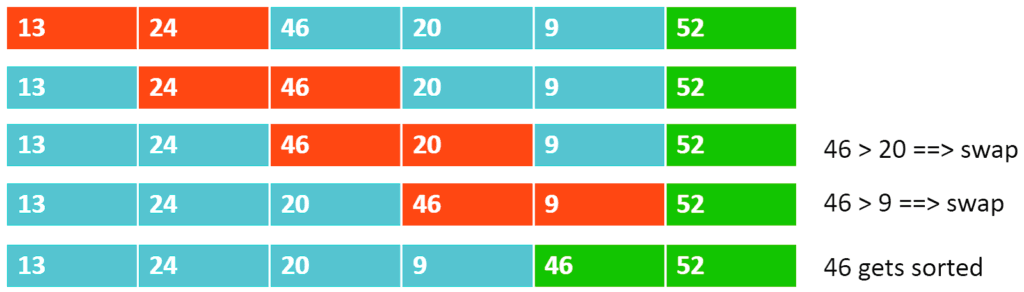
Recursion 3: bubble_sort(arr, 4):

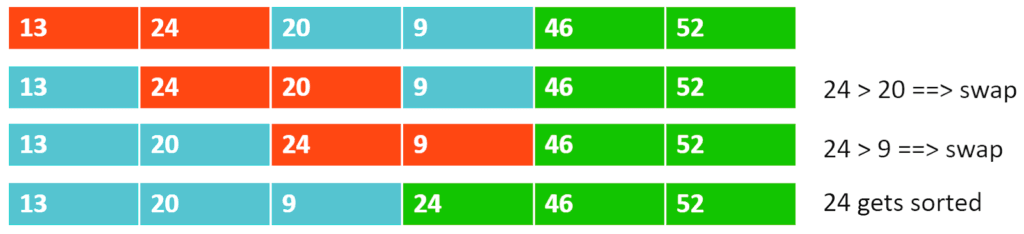
Recursion 4: bubble_sort(arr, 3):

Recursion 5: bubble_sort(arr, 2):

Recursion 6: bubble_sort(arr, 1):
Now, the recursion will hit the base case and it will return from this step.

The Code: Implementing Recursive Bubble Sort

Here’s a C++ implementation of the Recursive Bubble Sort:

#include <bits/stdc++.h>
using namespace std;

void bubble_sort(int arr[], int n) {
    // Base Case: range == 1.
    if (n == 1) return;

    for (int j = 0; j <= n - 2; j++) {
        if (arr[j] > arr[j + 1]) {
            int temp = arr[j + 1];
            arr[j + 1] = arr[j];
            arr[j] = temp;
        }
    }

    //Range reduced after recursion:
    bubble_sort(arr, n - 1);
}

int main()
{
    int arr[] = {13, 46, 24, 52, 20, 9};
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << "Before Using Bubble Sort: " << endl;
    for (int i = 0; i < n; i++)
    {
        cout << arr[i] << " ";
    }
    cout << endl;

    bubble_sort(arr, n);
    cout << "After Using bubble sort: " << "\n";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout << "\n";
    return 0;

}

Output:
Before Using Bubble Sort:
13 46 24 52 20 9
After Using bubble sort:
9 13 20 24 46 52

Time Complexity: O(N²), (where N = size of the array), for the worst, and average cases.

Reason: If we carefully observe, we can notice that the recursion call, is occurring for n times, and for each recursion call, the loop j runs from 0 to n-2. For, the range of size n, the inner loop runs n-1 times, for the range of size n-1, the inner loop runs n-2 times, and so on. So, the total steps will be approximately the following: (n-1) + (n-2) + (n-3) + ……..+ 3 + 2 + 1. The summation is approximately the sum of the first n natural numbers i.e. (n*(n+1))/2. The precise time complexity will be O(n²/2 + n/2). Previously, we have learned that we can ignore the lower values as well as the constant coefficients. So, the time complexity is O(n²). Here the value of n is N i.e. the size of the array.

Space Complexity: O(N) auxiliary stack space.

Optimized approach (Reducing time complexity for the best case):

The best case occurs if the given array is already sorted. We can reduce the time complexity to O(N) by just adding a small check inside the recursive function. 

• We will check in the first recursion call if any swap is taking place. If the array is already sorted no swap will occur and we will return from the recursion call. 
• Thus the number of recursions will be just 1. And our overall time complexity will be O(N).

Code:

#include <bits/stdc++.h>
using namespace std;

void bubble_sort(int arr[], int n) {
    // Base Case: range == 1.
    if (n == 1) return;

    int didSwap = 0;
    for (int j = 0; j <= n - 2; j++) {
        if (arr[j] > arr[j + 1]) {
            int temp = arr[j + 1];
            arr[j + 1] = arr[j];
            arr[j] = temp;
            didSwap = 1;
        }
    }

    // if no swapping happens.
    if (didSwap == 0) return;

    //Range reduced after recursion:
    bubble_sort(arr, n - 1);
}

int main()
{
    int arr[] = {13, 46, 24, 52, 20, 9};
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << "Before Using Bubble Sort: " << endl;
    for (int i = 0; i < n; i++)
    {
        cout << arr[i] << " ";
    }
    cout << endl;

    bubble_sort(arr, n);
    cout << "After Using bubble sort: " << "\n";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout << "\n";
    return 0;
}

Output:
Before Using Bubble Sort:
13 46 24 52 20 9
After Using bubble sort:
9 13 20 24 46 52 

Time Complexity: O(N²) for the worst and average cases and O(N) for the best case. Here, N = size of the array.

Space Complexity: O(N) auxiliary stack space.

Performance Analysis

• Time Complexity: The time complexity for the worst and average cases is O(N2)O(N^2)O(N2) because each recursive call processes the array in a linear fashion, leading to a quadratic number of operations.
• Best Case: The best case occurs when the array is already sorted. With a small tweak to check for swaps, we can optimize this to O(N)O(N)O(N).
• Space Complexity: The space complexity is O(N)O(N)O(N) due to the auxiliary stack space used by recursion.

Final Thoughts

Recursive Bubble Sort is not the most efficient sorting method out there, but it offers an engaging way to understand recursion and sorting principles. It’s a great exercise for those looking to strengthen their programming skills.

Have you tried implementing Recursive Bubble Sort or faced challenges with other sorting algorithms? Share your experiences or any additional techniques you’ve found helpful in the comments below!

Follow for more insights and updates on AI trends, techniques, and tips to enhance your understanding of the field!